I. Sissejuhatus
Kas vesi võib küünlaid süüdata? See on tõsi!
Kas on tõsi, et maod kardavad realgaari? See on vale!
Mida me täna arutama hakkame, on järgmine:
Kas interferents võib parandada mõõtmistäpsust?
Tavapärastes tingimustes on interferents mõõtmise loomulik vaenlane. Interferents vähendab mõõtmise täpsust. Rasketel juhtudel ei teostata mõõtmist tavapäraselt. Sellest vaatenurgast võib interferents parandada mõõtmise täpsust, mis on vale!
Aga kas see on alati nii? Kas on olemas olukordi, kus interferents ei vähenda mõõtmise täpsust, vaid hoopis parandab seda?
Vastus on jah!
2. Sekkumise leping
Arvestades tegelikku olukorda, lepime sekkumise osas kokku järgmise:
- Häired ei sisalda alalisvoolu komponente. Tegelikus mõõtmises on häiringuks peamiselt vahelduvvoolu häire ja see eeldus on mõistlik.
- Võrreldes mõõdetud alalisvoolupingega on interferentsi amplituud suhteliselt väike. See on kooskõlas tegeliku olukorraga.
- Häire on perioodiline signaal ehk keskmine väärtus on fikseeritud ajaperioodi jooksul null. See punkt ei pruugi tegeliku mõõtmise puhul tõele vastata. Kuna aga häiringuks on üldiselt kõrgema sagedusega vahelduvvoolusignaal, on enamiku häiringute puhul mõistlik pikema ajaperioodi jooksul nullkeskmist väärtust pidada.
3. Mõõtmistäpsus häirete korral
Enamik elektrilisi mõõteriistu ja arvesteid kasutab nüüd AD-muundureid ning nende mõõtmistäpsus on tihedalt seotud AD-muunduri eraldusvõimega. Üldiselt on suurema eraldusvõimega AD-muunduritel suurem mõõtmistäpsus.
Siiski on AD-muunduri eraldusvõime alati piiratud. Eeldades, et AD-muunduri eraldusvõime on 3 bitti ja kõrgeim mõõtepinge on 8 V, on AD-muundur samaväärne skaalaga, mis on jagatud 8 jaotuseks, iga jaotus on 1 V. Selle AD-muunduri mõõtetulemus on alati täisarv ja kümnendosa kantakse alati üle või jäetakse kõrvale, mida käesolevas artiklis eeldatakse. Ülekandmine või jätmine põhjustab mõõtmisvigu. Näiteks 6,3 V on suurem kui 6 V ja väiksem kui 7 V. AD mõõtetulemus on 7 V ja viga on 0,7 V. Me nimetame seda viga AD kvantimisveaks.
Analüüsi mugavuse huvides eeldame, et skaalal (AD-muunduril) pole muid mõõtmisvigu peale AD-kvantimisvea.
Nüüd kasutame kahte sellist identset skaalat joonisel 1 näidatud kahe alalispinge mõõtmiseks ilma häireteta (ideaaljuhul) ja häiretega.
Nagu joonisel 1 näidatud, on tegelik mõõdetud alalispinge 6,3 V ja vasakpoolsel joonisel oleval alalispingel puuduvad häired ning see on konstantse väärtusega. Parempoolne joonis näitab vahelduvvoolu poolt häiritud alalisvoolu ja selle väärtuses esineb teatav kõikumine. Parempoolsel diagrammil olev alalispinge on pärast häirete kõrvaldamist võrdne vasakpoolsel diagrammil oleva alalispingega. Punane ruut joonisel tähistab AD-muunduri muundamise tulemust.

Ideaalne alalispinge ilma häireteta
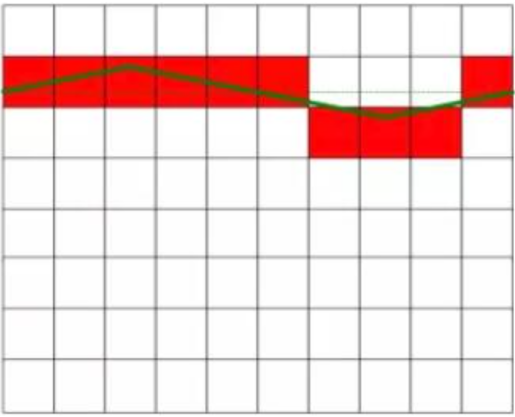
Rakenda häirivat alalispinget, mille keskmine väärtus on null
Tehke ülaltoodud joonisel kujutatud kahel juhul 10 alalisvoolu mõõtmist ja seejärel arvutage 10 mõõtmise keskmine.
Vasakpoolset esimest skaalat mõõdetakse 10 korda ja näidud on iga kord samad. AD-kvantimisvea mõju tõttu on iga näit 7V. Pärast 10 mõõtmise keskmistamist on tulemus ikkagi 7V. AD-kvantimisviga on 0,7V ja mõõtmisviga on 0,7V.
Teine skaala paremal on dramaatiliselt muutunud:
Interferentsipinge ja amplituudi positiivse ja negatiivse erinevuse tõttu on AD kvantimisviga erinevates mõõtepunktides erinev. AD kvantimisvea muutumisel muutub AD mõõtmistulemus 6 V ja 7 V vahel. Seitse mõõtmist olid 7 V, ainult kolm olid 6 V ja 10 mõõtmise keskmine oli 6,3 V! Viga on 0 V!
Tegelikult pole ükski viga võimatu, sest objektiivses maailmas pole rangelt 6,3 V! Siiski on neid:
Häirete puudumisel, kuna iga mõõtmistulemus on sama, jääb viga pärast 10 mõõtmise keskmistamist samaks!
Kui interferentsi hulk on piisav, siis pärast 10 mõõtmise keskmistamist väheneb AD-kvantimisviga suurusjärgu võrra! Eraldusvõime paraneb suurusjärgu võrra! Ka mõõtmise täpsus paraneb suurusjärgu võrra!
Põhiküsimused on järgmised:
Kas see on sama, kui mõõdetud pinge on teistsugune?
Lugejad võivad soovida järgida teises osas interferentsi käsitlevat kokkulepet, väljendada interferentsi numbriliste väärtuste jadana, kanda interferents mõõdetud pingele ja seejärel arvutada iga punkti mõõtmistulemused AD-muunduri kandepõhimõtte kohaselt ning seejärel arvutada kontrollimiseks keskmise väärtuse, kui interferentsi amplituud võib põhjustada AD-kvantimise järgse näidu muutuse ja diskreetimissagedus on piisavalt kõrge (interferentsi amplituudi muutustel on üleminekuprotsess, mitte kaks positiivset ja negatiivset väärtust) ning täpsust tuleb parandada!
On tõestatav, et seni, kuni mõõdetud pinge ei ole täpselt täisarv (see ei eksisteeri objektiivmaailmas), tekib AD kvantimisviga, olenemata AD kvantimisvea suurusest. Seni kuni interferentsi amplituud on suurem kui AD kvantimisviga või suurem kui AD minimaalne lahutusvõime, põhjustab see mõõtmistulemuse muutumise kahe külgneva väärtuse vahel. Kuna interferents on positiivselt ja negatiivselt sümmeetriline, on vähenemise ja suurenemise suurus ja tõenäosus võrdsed. Seega, kui tegelik väärtus on lähemal millisele väärtusele, on millise väärtuse ilmnemise tõenäosus suurem ja see on pärast keskmistamist millise väärtuse lähedal.
See tähendab: mitme mõõtmise keskmine väärtus (interferentsi keskmine väärtus on null) peab olema interferentsivabale mõõtmistulemusele lähemal, st vahelduvvoolu interferentsisignaali kasutamine keskmise väärtusega null ja mitme mõõtmise keskmistamine võib vähendada samaväärseid AD kvantiseerimisvigu, parandada AD mõõtmise eraldusvõimet ja parandada mõõtmise täpsust!
Postituse aeg: 13. juuli 2023




